|
|
Modele pulsacyjne dla gwiazd o masach od 1.6 do 20 MSun wyznaczone przy użyciu nieprzeźroczystości OP
J. Daszyńska-Daszkiewicz, P. Walczak, Instytut Astronomiczny, Uniwersytet Wrocławski
In all computations the OPAL equation of state were used.
Pobierz:
- OP, A04, X = 0.65, Z = 0.020, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.010, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.015, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.020, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.020, AC = 0, AO = 0, V = 200
- OP, A04, X = 0.75, Z = 0.020, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.030, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.020, AC = 0, AO = 0, V = 50
- OP, A04, X = 0.70, Z = 0.020, AC = 0, AO = 0, V = 100
- OP, A04, X = 0.70, Z = 0.015, AC = 0, AO = 0, V = 50
- OP, A04, X = 0.70, Z = 0.015, AC = 0, AO = 0, V = 100
- OP, A04, X = 0.70, Z = 0.015, AC = 0, AO = 0, V = 200
- OP, A04, X = 0.65, Z = 0.015, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.015, AC = 0, AO = 0, V = 50
- OP, A04, X = 0.70, Z = 0.009, AC = 0, AO = 0, V = 0
- OP, A04, X = 0.70, Z = 0.02, AC = 0, AO = 0, V = 50
| OP | – | OP opacities (Seaton 2005) |
| A04 | – | Chemical Composition (Asplund 2004) |
| X | – | hydrogen abundance |
| Z | – | heavy element abundance |
| AC | – | MLT parameter (mixing-length theory); AC = alpha convective = lconv/Hp, where lconv - mixing length, Hp - local pressure scale height |
| AO | – | convective overshooting parameter; AO = alpha overshooting = dover/Hp, where dover - convective overshooting |
| V | – | initial equatorial rotational velocity [km/s] |
Stellar oscillations were calculated from ZAMS to TAMS. The oscillation
files are called nad***.mrt, and are packed for each mass. The structure of
these files is as follows:
first line:
M=... Teff=... logL=... R=... logg=... Vrot=...
where
| M | – | the stellar mass in solar units |
| Teff | – | logTeff |
| logL | – | logL/L๏ |
| R | – | the stellar radius in solar units |
| logg | – | logg |
second line:
| l |
n |
sig |
P[hrs] |
fa[c/d] |
fn[c/d] |
COMPLEX F |
ekg/ek |
eta |
where
| l | – | the spherical harmonic degree, l |
| n | – | the radial order, n |
| sig | – | | the dimensionless frequency defined as | 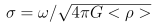 |
|
| P[hrs] | – | oscillation period in [h] |
| fa[c/d] | – | adiabatic oscillation frequency in [c/d] |
| fn[c/d] | – | adiabatic oscillation frequency in [c/d] |
| COMPLEX F | – | (two values) the ratio of the radiative flux perturbation to the radial displacement at the level of the photosphere |
| ekg/ek | – | ratio of the gravitational energy to the total kinetic energy; 0 for "pure" pressure modes, 1 for "pure" gravity modes |
| eta | – | | instability parameter defined as η = | 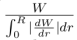 |
|
| |
where W is the work integral. For unstable modes we have η > 0. The values of the η parameter
change from -1 (damping everywhere) to +1 (driving everywhere)
|
|